Pii: s0378-5173(99)00147-7

International Journal of Pharmaceutics 186 (1999) 119 – 125 A compartmental absorption and transit model for a Glaxo Wellcome Inc., Fi6e Moore Dri6e, Research Triangle Park, NC 27709, USA b College of Pharmacy, The Uni6ersity of Michigan, Ann Arbor, MI 48109, USA Received 2 November 1998; received in revised form 16 April 1999; accepted 19 April 1999 Abstract
This report describes a compartmental absorption and transit model to estimate the fraction of dose absorbed and the rate of drug absorption for passively transported drugs in immediate release products. The model considerssimultaneous small intestinal transit flow and drug absorption. Both analytical and numerical methods were utilizedto solve the model equations. It was found that the fraction of dose absorbed can be estimated by F = 1 − (1 + 0.54 is the human effective permeability in cm/h. A good correlation was found between the fraction of dose absorbed and the effective permeability for ten drugs covering a wide range of absorption characteristics. Themodel was able to explain the oral plasma concentration profiles of atenolol. 1999 Elsevier Science B.V. All rightsreserved.
Keywords: Drug absorption kinetics; Fraction of dose absorbed; Permeability; Compartmental modeling 1. Introduction
mechanistic models have been discussed in a re-cent review article (Yu et al., 1996a). Although Estimating intestinal drug absorption kinetics gastric emptying and small intestinal transit flow can greatly facilitate lead drug candidate selection can influence the rate and extent of drug absorp- and support formulation strategies. Quantitative tion after oral administration, none of the previ- and mechanistic approaches have been developed ous models have fully considered these factors.
since the traditional approach to treat the entire The aim of this report was to develop a compart- gastrointestinal tract as a single-compartment mental absorption and transit (CAT) model for ‘black box’ does not suffice (Ho et al., 1983; estimating the fraction of dose absorbed and the Dressman et al., 1984; Sinko et al., 1991). The rate of drug absorption based on the transit mod- utilities and limitations of these quantitative and els (Yu et al., 1996b; Yu and Amidon, 1998). Wederived an equation to correlate the fraction ofdose absorbed with the human effective perme- * Corresponding author. Tel.: + 1-919-4830445; fax: + 1- ability. The CAT model was related to compart- E-mail address: lxy33016@glaxo.com (L.X. Yu) mental pharmacokinetic models to evaluate the 0378-5173/99/$ - see front matter 1999 Elsevier Science B.V. All rights reserved.
PII: S 0 3 7 8 - 5 1 7 3 ( 9 9 ) 0 0 1 4 7 - 7 L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 effect of gastric emptying on plasma concentra- 2. Theoretical
where M is the amount of drug in the stomach, M is the amount of drug in the colon, M is the Fig. 1 illustrates the CAT model to account for amount of drug in the nth compartment, t is the the transit flow in the stomach, duodenum, je- time, K , K , and K are the rate constants of junum, and ileum, and the passive absorption in gastric emptying, small intestinal transit, and in- the duodenum, jejunum, and ileum. The gas- trinsic absorption, respectively. In Eq. (2), when trointestinal tract is divided into three segments: n = 1, the term K M is replaced by K M . The stomach, small intestine, and colon. The transit rate of drug absorption from the small intestine flow in the human small intestine can be described by seven compartments, where a drug transfers from one compartment to the next one in a first-order fashion (Yu et al., 1996b). The colon is considered only as a reservoir and the colonic where M is the amount of drug absorbed. From transit flow was not considered in this model. The 1. Absorption from the stomach and colon is insignificant compared with that from the As t “, M and M ’s approach zero, so 2. Transport across the small intestinal mem- The fraction of dose absorbed, F , can then be 4. A drug moving through the small intestine can be viewed as a process flowing through a series of segments, each described by a single com- partment with linear transfer kinetics from one to next, and all compartments may have dif- Coupling with Eqs. (1) and (2), the analytical ferent volumes and flow rates, but have the same residence times (Yu and Amidon, 1998).
Therefore, for a non-degradable drug dosed in an immediate release dosage form, the absorption and transit in the gastrointestinal tract can bedepicted as follows.
Fig. 1. A schematic diagram of the CAT model with lineartransit and passive absorption kinetics. This model accounts for the transit in the stomach, duodenum, jejunum, and ileum, and the absorption in the duodenum, jejunum, and ileum.
L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 The transit rate constant K can be estimated from 3. Methods
the mean small intestinal transit time (Yu et al.,1996b): Model 1 – 3 and 13 – 15 are a typical initial value problem of an ordinary differential equation sys-tem. This system was numerically solved by the The absorption rate constant K is proportional ADAPT pharmacokinetic and pharmacodynamic to the effective permeability, P , (Sinko et al., modeling package (D’Argenio and Schumitzky, 1992). A subroutine was written to accommodate 3.2. Estimating fraction of dose absorbed where R is the radius of the small intestine. Thesubstitution of Eqs. (9) and (10) into Eq. (8) gives Ten compounds covering a wide range of ab- sorption characteristics, from enalaprilat (the least permeable) to ketoprofen (the most permeable), were chosen to evaluate the predictability of themodel. The permeability data were obtained from Substitution of ŽT  of 3.32 h (Yu et al., 1996b) regional perfusion studies in humans using the and the radius of 1.75 cm (Lennernas et al., 1992) regional intestinal perfusion technique (Lennernas et al., 1994; Amidon et al., 1995; Fagerholm et al.,1995; Lennernas et al., 1995; Amidon, 1996; Lin- dahl et al., 1995). The fraction of dose absorbeddata were obtained from the literature (Paterson where the human effective permeability P et al., 1970; Mason et al. 1979; Eichelbaum et al., expressed in cm/h. If there is no first pass effect, 1982; Davies, 1984; Kubo and Cody, 1985; Tse et Eq. (4) can be related to intravenous pharmacoki- al., 1992; Ponto and Schoenwald, 1993; Benet et netic models to estimate oral plasma concentra- al., 1996; American Hospital Formulary Service, tion profiles. For example, in the case of the 1998 Edition). The fraction of dose absorbed data three-compartment open model with central com- were corrected for first pass effects, if any. Table partment elimination (Wagner, 1993), we have the 3.3. Estimating rate of drug absorption In conjunction with the compartmental phar- macokinetics model Eqs. (12) – (15), the CAT model was used to simulate oral plasma concen- tration profiles of atenolol. Atenolol is a b -selec- tive b-adrenergic receptor blocking agent andessentially undergoes no first-pass metabolism (Riddell et al., 1987). Two simulations were car- ried out with respect to gastric emptying (mono-exponential and biphasic gastric emptying). The where V is the volume of the central compart- effective permeability of atenolol was found to be ment 1, and C , C , and C are the plasma con- 0.19 cm/h (Amidon et al., 1995). The volume of the central compartment and microscopic rate respectively. k , k , k , k , and k constants were taken from the intravenous phar- macokinetics study by Mason et al. (1979).
L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 dicted fraction of dose absorbed is 34%, slightly Summary of the literature data of permeability and fraction of below the experimental observations. The model predicted the fraction dose absorbed to be 48, 50, 84, and 95% for terbutaline, atenolol, metoprolol, and propranolol, respectively, based on the per- meability data. The predicted results are in agree- ment with the experimental data (Paterson et al., 1970; Mason et al., 1979; Davies, 1984; Benet et al., 1996; American Hospital Formulary Service, 1998). Fluvastatin, antipyrine, naproxen, and ke- toprofen are completely absorbed (Eichelbaum et al., 1982; Benet et al., 1996; Tse et al., 1992), as 4.2. Estimating the rate of drug absorption Fig. 3 gives the theoretical prediction (dotted lines) for rate of drug absorption, based on mono- exponential gastric emptying and the mean gastric residence time of 0.25 h for all three doses. The theoretical prediction is in fair agreement with the experimental data. The double peaks in the exper- a The oral bioavailability metoprolol is about 38% (Benet et imental plasma concentration profiles would not al., 1996). After oral dose, about 50% of dose appears to be expected from the simulation, however. Mason undergo first-pass metabolism in the liver (AHFS Drug Infor-mation, 1998, pp. 1369). Thus, the fraction of dose is about0.88.
b The oral bioavailability of propranolol is about 26%.
However, the drug is completely absorbed following oral doses(Paterson et al., 1970).
c The fraction of dose absorbed of fluvastatin is 0.93–0.98 although the oral bioavailability is only 19–29% due to exten-sive first-pass effect (Tse et al., 1992).
4. Results and discussion
4.1. Estimating fraction of dose absorbed Fig. 2 shows the predicted values. The fraction of dose absorbed for enalaprilat in laboratoryanimals was estimated to be only 5 – 12%; in hu-mans, oral absorption of radiolabelled enalaprilatwas probably less than 10% (Kubo and Cody,1985). The model predicted the fraction of doseabsorbed to be 26% for enalaprilat, higher than Fig. 2. The fraction of dose absorbed as a function of the the experimental value. The fraction of dose ab- human effective permeability, where ( — ) represents the pre- sorbed for furosemide varies from 37 to 83% in diction of the compartmental absorption and transit model, healthy volunteers and the mean value is around (---) represents the single compartment model, and (···), the 55% (Ponto and Schoenwald, 1993). 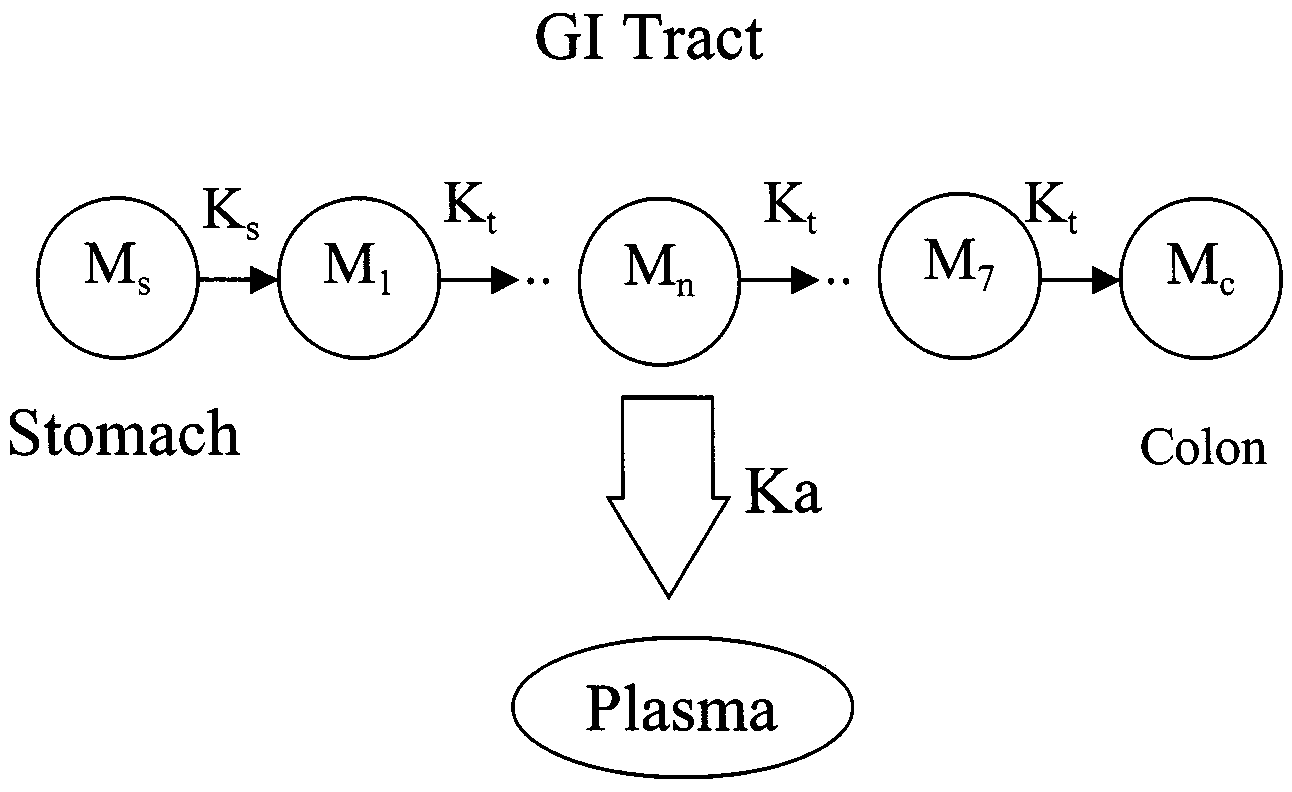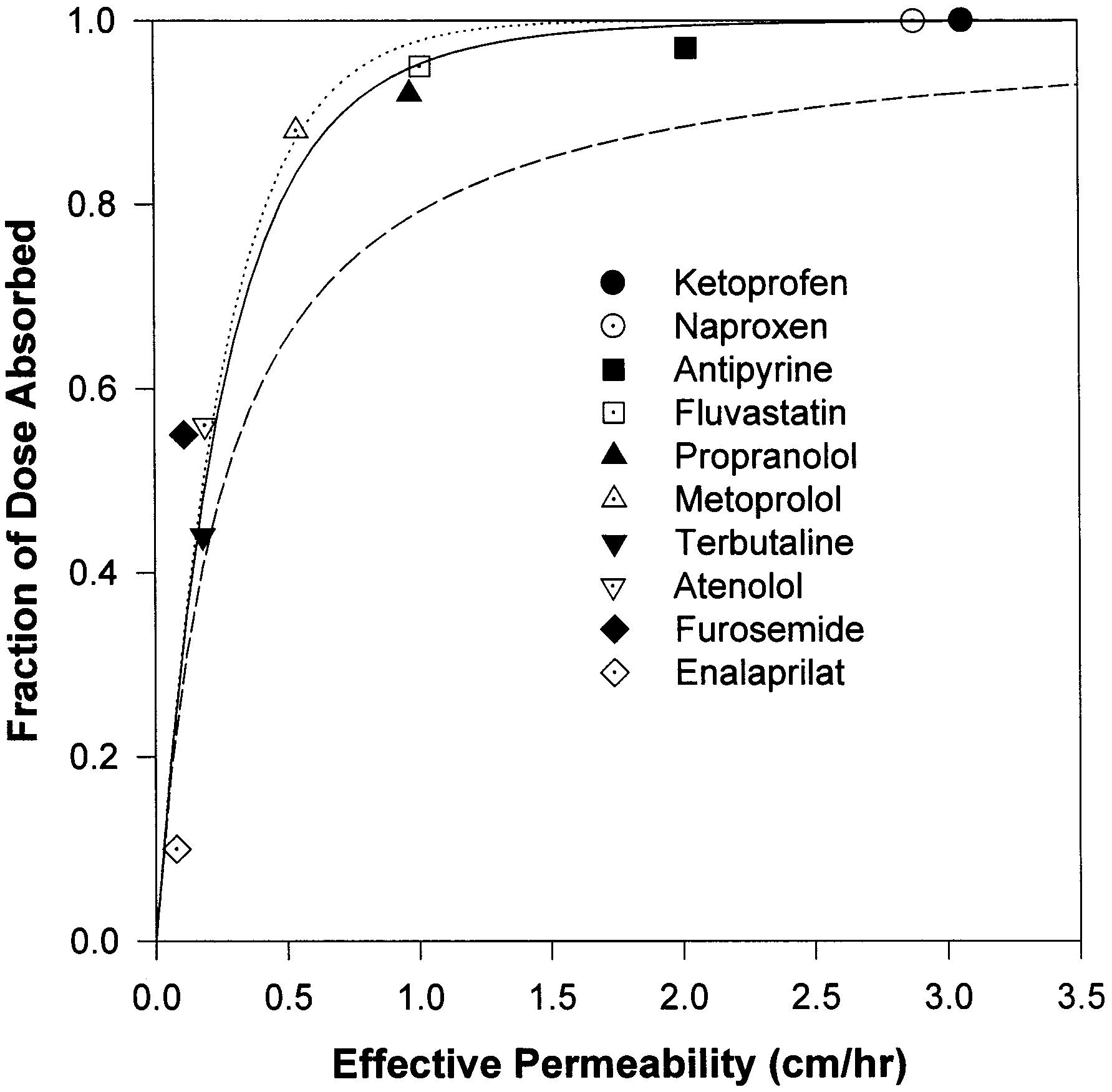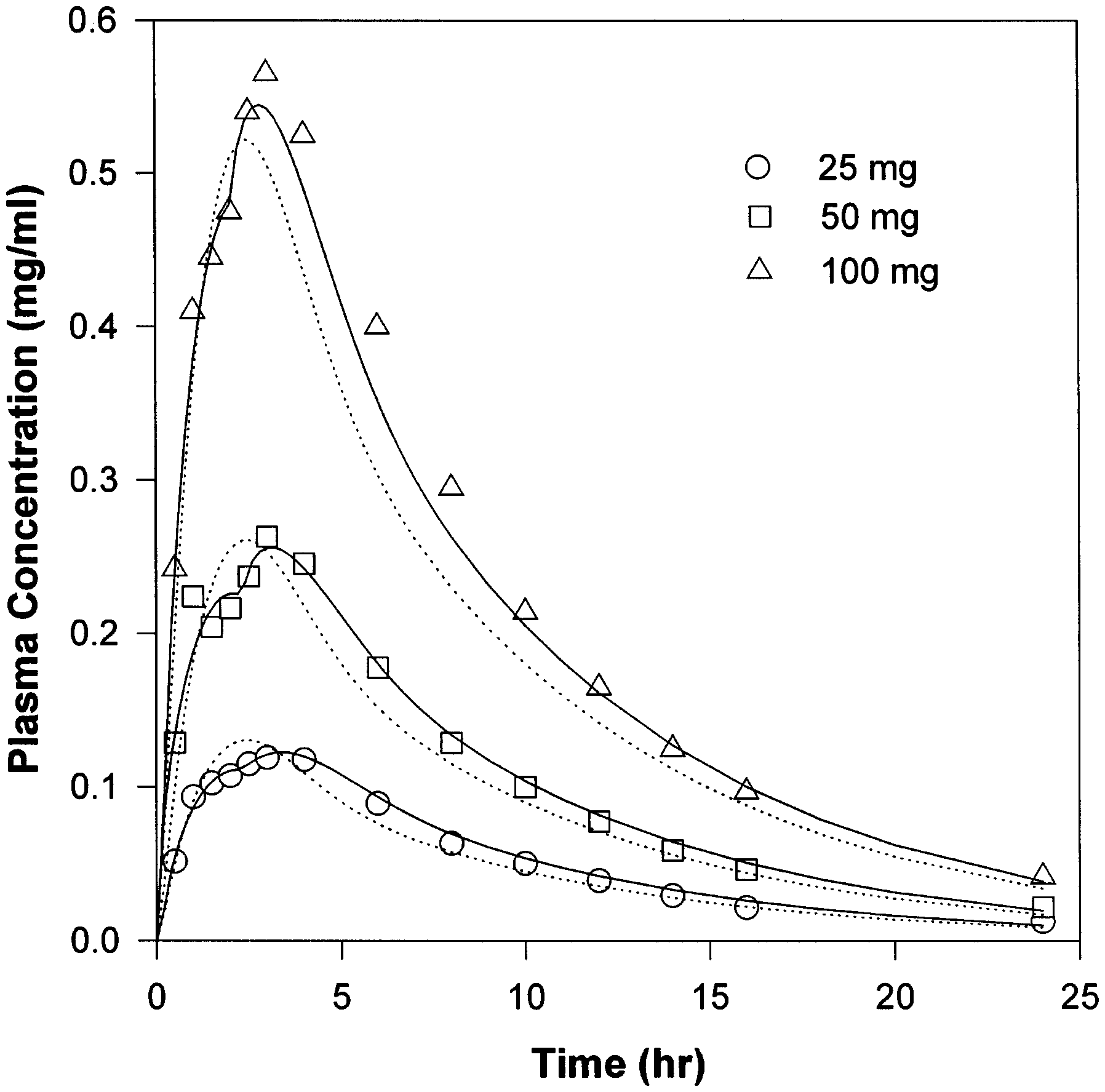The pre- L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 almost two hours of no emptying. The remainingdrug was completely cleared from the stomach inthe second phase of the emptying, producing thesecond peak in the plasma concentration profile.
Nevertheless, no gastric emptying for 2 hours isphysiologically questionable although not impos-sible despite the fact that the biphasic gastricemptying model is better than the monoexponen-tial model for fitting the experimental data.
Several approaches to predicting the fraction of dose absorbed have been discussed in the litera-ture (Yu et al., 1996a). Ho et al. (1983) developeda dispersion model and proposed an anatomicalreserve length concept. The dispersion model isphysically more plausible than the CAT model.
However, the current dispersion model is proba- Fig. 3. Prediction of plasma concentration profiles of atenolol bly unable to account for gastric emptying and to at the 25, 50, and 100 mg oral doses, where dotted lines simulate the effect of gastric emptying on absorp- represent the prediction with monoexponential gastric emp-tying, solid lines represent the prediction with biphasic gastric tion (Yu et al., 1996b). The dispersion model also emptying (two intervals of monoexponential emptying, inter- appears to be difficult to incorporate into phar- rupted by an interval with no emptying), and symbols repre- macokinetic models to estimate plasma concentra- sent the experimental results from Mason et al. (1979).
Sinko et al. (1991) developed a macroscopic et al. (1979) postulated that the biphasic gastric mass balance approach and showed the relation- emptying contributed to the double peaks.
ship between the fraction of dose absorbed and In the next simulation, therefore, we assumed the absorption number (effective permeability) that the drug was emptied from the stomach in a under steady-state conditions. Two flow models biphasic fashion. The simulation results are also were considered in the mass balance approach: shown in Fig. 3. Evidently, there exist double the single mixing tank model and the plug flow peaks in the simulated curves (solid lines). Based model. The single mixing tank model, as the name on the F-test, the pharmacokinetic model with suggests, considers the small intestinal tract a biphasic gastric emptying was found to be a sig- mixed tank with uniform concentration. The plug nificant improvement over the model with mono- flow model considers the small intestinal tract a uniform tube without axial mixing. In the case of The parameters in the biphasic gastric emptying the single mixing tank model, the mass balance include two rate constants and the interval be- tween the two phases (Clements et al., 1978, type 3). The first phase of the biphasic gastric emp- tying was assumed to have the same rate constantas the monoexponential emptying. The values of In the case of the plug flow model, the mass the second emptying phase and the interval were determined by curve fitting. In a typical simula- F = 1 − e−3.87 Peff.
tion, approximately 77% of the dose was evacu-ated from the stomach during the first phase. The Fig. 2 shows the fraction of dose absorbed emptying was then interrupted by an interval of calculated by Eqs. (16) and (17). The single com- L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 partment model underestimates the fraction of D’Argenio, D.Z., Schumitzky, A. 1992. Adapt II: Mathemat- dose absorbed whereas the plug flow and the ical Software for Pharmacokinetics/PharmacodynamicsSystems Analysis, University of Southern California, Los CAT models give a much closer fit to the data.
We have shown that the CAT based pharmacoki- Davies, D.S., 1984. Pharmacokinetics of terbutaline after oral netic model was able to incorporate gastric emp- administration. Eur. J. Resp. Dis. Suppl. 134, 111 – 117.
tying and predict plasma concentration profiles.
Dressman, J.B., Fleisher, D., Amidon, G.L., 1984. Physico- This appears to be difficult to achieve by the plug chemical model for dose-dependent drug absorption. J.
flow model because of its steady state assumption.
Eichelbaum, E., Ochs, H.R., Roberts, G., Somogyi, A., 1982.
Pharmacokinetics and metabolism of antipyrine after in-travenous and oral administration. Arzneim-Forsch. 32, 5. Conclusions
Fagerholm, U., Borgstrom, L., Ahrenstedt, O., Lennernas, This report describes a compartmental absorp- H., 1995. The influence of net water absorption on thesmall intestinal permeability of terbutaline, studied in tion and transit model to estimate oral drug ab- vivo in man. J. Drug Target. 3, 191 – 200.
sorption of passively transported drugs. A simple Ho, N.F.H., Park, J.Y., No, P.F., Higuchi, W.I., 1983. Ad- equation was derived which predicts the fraction vanced quantitative and mechanistic approaches in inter- of dose absorbed reasonably well. The CAT facing gastrointestinal drug absorption studies in animals model offers the advantages of being able to and humans. In: Crouthanel, W., Sarapu, A.C. (Eds.), estimate the rate of drug absorption and couple Animal Models for Oral Drug Delivery in Man: In Situand In Vivo Approaches. American Pharmaceutical Asso- ciation, Washington, DC, pp. 27 – 106.
models. The simulation study showed that gastric Kubo, S.H., Cody, R.J., 1985. Clinical pharmacokinetics of emptying could cause double peaks in oral plasma the angiotensin converting enzyme inhibitors. Clin. Phar- Lennernas, H., Ahrenstedt, O., Hallgren, R., Knutson, L., Ryde, M., Paalzow, L.K., 1992. Regional jejunal perfu-sion, a new in vivo approach to study oral drug absorp- Acknowledgements
tion in man. Pharm. Res. 9, 1243 – 1251.
Lennernas, H., Ahrenstedt, O., Ungel, A.-L., 1994. Intestinal The authors would like to thank Avis Bridgers, drug absorption during induced net water absorption in Ambrish Vyas, and Mark Sacchetti for reviewing man: A mechanistic study using antipyrine, atenolol andenalaprilat. Br. J. Clin. Pharmacol. 37, 589 – 596.
Lennernas, H., Knutson, L., Knutson, T., Lesko, L., Salmonson, T., G.L. Amidon, G.L. 1995. Human effec-tive permeability data for furosemide, hydrochlortiazide, References
ketoprofen, and naproxen to be used in the proposedbiopharmaceutical classification for IR-products. Pharm.
Res. 12, S396.
American Hospital Formulary Service. 1998 Edition, pp.
Lindahl, A., Sandstrom, R., Ungell, A.-L., Knutsson, L., Amidon, G.L., Lennernas, H., Shah, V.P., Crison, J.R., Abrahamsson, B., Lennernas, H.A., 1995. Human study 1995. A theoretical basis for a biopharmaceutic drug clas- of the regional jejunal effective permeability of fluvas- sification: the correlation of in vitro drug product dissolu- tatin, atenolol, metoprolol, and antipyrine. Pharm. Res.
Mason, W.D., Winer, N., Kochak, G., Cohen, I., Bell, R., Amidon, G.L., 1996. Unpublished results.
1979. Kinetics and absolute bioavailability of atenolol.
Benet, L.Z., (ie, S., Schwartz, J.B., 1996. Design and opti- Clin. Pharmacol. Ther. 25, 408 – 415.
mization of dosage regiments; pharmacokinetic data. In: Paterson, J.W., Conolly, M.E., Dollery, C.T., Hayes, A., Hardman, J.G., Limbird, L.E., Gilman, A.G. (Eds.), The Pharmacological Basis of Therapeutics, 9th edition. Mc- metabolism of propranolol in man. Pharmacol. Clin. 2, Graw-Hill, New York, pp. 1707 – 1793.
Clements, J.A., Heading, R.C., Nimmo, W.S., Prescott, L.F., Ponto, L.L.B., Schoenwald, R.D., 1993. Furosemide: a phar- 1978. Kinetics of acetaminophen absorption and gastric macokinetics/pharmacodynamic review. Clin. Pharma- emptying in man. Clin. Pharmacol. Ther. 24, 420 – 431.
L.X. Yu, G.L. Amidon / International Journal of Pharmaceutics 186 (1999) 119 – 125 Riddell, J.G., Harron, D.W.G., Shanks, R.G., 1987. Clinical Yu, L.X., Crison, J.R., Amidon, G.L., 1996a. Transport ap- pharmacokinetics of b-adrenoceptor antagonists. Clin.
proaches to the biopharmaceutical design of oral drug delivery systems: prediction of oral drug absorption. Adv.
Sinko, P.J., Leesman, G.D., Amidon, G.L., 1991. Predicting fraction dose absorbed in humans using a macroscopic Yu, L.X., Crison, J.R., Amidon, G.L., 1996b. Compart- mass balance approach. Pharm. Res. 8, 979 – 988.
mental transit and dispersion model analysis of small Tse, F.L.S., Jaffe, J.M., Troendle, A., 1992. Pharmacokinetics intestinal transit flow in humans. Int. J. Pharm. 140, of fluvastatin after single and multiple doses in normal volunteers. J. Clin. Pharmacol. 32, 630 – 638.
Yu, L.X., Amidon, G.L., 1998. Characterization of small Wagner, J.G. 1993. Pharmacokinetics for the Pharmacokineti- intestinal transit time distribution in humans. Int. J.
cal Scientists; Technomic Publishing, Inc. pp. 45 – 50.

Source: http://www.biosym.uzh.ch/modules/models/PBPK_Model/model_for_estimating_oral_drug_absorption.pdf